Rigid Registration¶
A rigid transform can register objects that are related by rotation and translation. For example, if you are registering images of a patient’s bones, you can often assume that a rigid transform is sufficient to align these structures. In fact, it is often advantageus to chose a simple transform if problems that allows it, as this constrains the solution space and ensures no spurious non-rigid local minima affect your results. Think of it as a way of embedding expert knowledge in the registration procedure.
Tip
Rigid registration is one of the simplest of methods in the catagory of linear transformation models and is often used as initialization for affine- and non-rigid transforms.
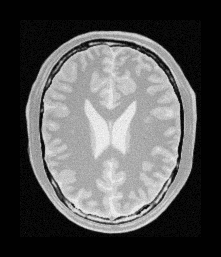
The rigid transform is selected using (Transform "EulerTransform"). Consider the images in Figure 8.
The image on right has been rotated 10 degrees and translated 13 pixels in the x-direction and 17 pixels in the y-direction. Using the EulerTransform we may correct for this misalignment.
import SimpleITK as sitk
elastixImageFilter = sitk.ElastixImageFilter()
elastixImageFilter.SetFixedImage(sitk.ReadImage("fixedImage.nii"))
elastixImageFilter.SetMovingImage(sitk.ReadImage("movingImage.nii"))
elastixImageFilter.SetParameterMap(sitk.GetDefaultParameterMap("rigid"))
elastixImageFilter.Execute()
sitk.WriteImage(elastixImageFilter.GetResultImage())
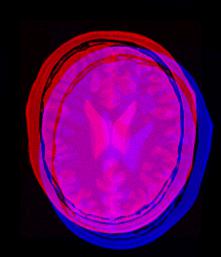
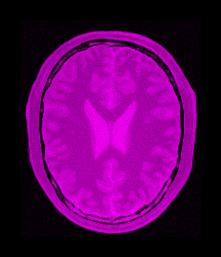
It is clear from the result mean image on right in Fig. 9 that registration was successful.
In the next example we will introduce scaling and shearing into the registration.